|
|
|
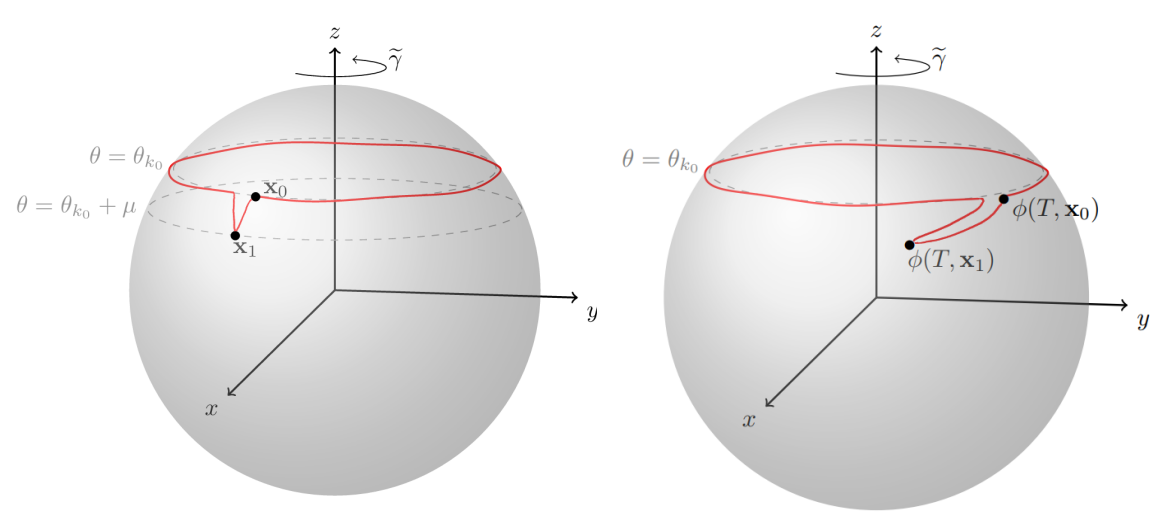
RésumésThis webpage will be updated regularly. Title: Lois de conservation et équations aux dérivées partielles dispersives Abstract: Les lois de conservation font partie intégrante de la théorie des systèmes d'EDP hyperboliques au travers de la notion d'entropie. Il est sans doute moins connu que des systèmes de lois de conservation sont associés aux EDP dispersives. Appelées équations de modulation, ces lois sont rarement explicites. Si elles sont relativement bien comprises pour les EDP intégrables telles que l'équation de Korteweg--de Vries, l’étude des équations de modulation en est encore à ses balbutiements pour les EDP dispersives non intégrables. Dans cet exposé, je présenterai un aperçu de résultats récents et de questions ouvertes. Title: a-contraction theory for systems satisfying some Kawashima conditions Abstract: Shock formation is a known feature of many hyperbolic systems of conservation laws. Shocks are also known to be crucial building blocks in the construction of solutions to hyperbolic equations. Thus, in order to understand the vanishing viscosity problem from hyperbolic-parabolic equations to hyperbolic equations, the study of the stability of viscous shocks is crucial. The a-contraction theory aims at providing a framework to study the stability of such waves and other patterns. This theory aims at deriving some control on the distance between a solution to the system and a chosen translation of a given viscous shock. In particular, I will discuss how to derive such estimates for systems satisfying conditions of Kawashima class. This is based on a joint work with Alexis Vasseur. Title: Entropy methods for the fermionic Boltzmann equation Abstract: The Boltzmann equation describes a gas as a large collection of molecules, with a statistical point a view. The Boltzmann-Fermi-Dirac equation (fermionic Boltzmann) is a quantum variant which includes the Pauli exclusion principle, suited to describe distributions of electrons in semi-conductors. The obtention of explicit rates of convergence towards equilibrium are challenging. A widely used tool for this kind of problem is the entropy method, which relies on functional inequalities. For the Boltzmann equation, such inequalities were obtained around the 2000’s notably by Desvillettes, Toscani, and Villani. In order to obtain similar inequalities for the Boltzmann-Fermi-Dirac equation, we developed a method of transfer, showing that any such inequality holding in the case of the Boltzmann equation also holds for the Boltzmann-Fermi-Dirac equation. We then obtain (in collaboration with B. Lods) the first quantitative rate of convergence to equilibrium of the solutions to the Boltzmann-Fermi-Dirac equation for hard potentials with cutoff. Title: Heat flow, log concavity, and functional inequalities Abstract: In this talk I am presenting a few results about the classical heat flow, obtained in collaboration with Francesco Pedrotti in 2024. It is a well-known fact that compactly supported initial data become (definitely) log-concavity along the heat flow. I will address the same issue of “creation of log-concavity” for more general initial data. Applications are discussed to functional inequalities and score-based diffusions in statistics. Title: The weak approximation problem for manifold-valued Sobolev mappings. Abstract: In a striking contrast with the classical situation of real-valued Sobolev functions, a Sobolev mapping taking its values into a manifold N need not be a limit of smooth N-valued maps with respect to the strong convergence. A natural idea to try restoring the approximation property by smooth maps is to work with a weaker notion of convergence. Unlike the strong approximation problem, which is by now considered as well-understood, the picture of the weak approximation problem remains yet widely open. In this talk, I will present the history of this problem, some well-known results, as well as some recent progress. Title: Aronson-Benilan estimates for the Keller-Segel system Abstract: The Aronson-Benilan estimate, well known for the porous media equation ∂t ρ−Δ ρm=0 provides a lower bound on the Laplacian of pressure: Δρm−1 ≥ C. In this talk, I will show that this estimate remains valid for another equation: the Keller-Segel equation, which is a porous medium equation to which we add an aggregation term. Among other things, this provides a new proof of global existence for this system. I will focus on the two dimensional case, with a linear diffusion and with a small initial mass but the result can be extended for any dimension, with the critical diffusion exponent and up to and including the critical mass. This work is in collaboration with Alejandro Jimenez-Fernandez and Filippo Santambrogio. Title: Linear Landau Damping in a Vlasov-Euler system for Thick Sprays Abstract: We are interested in the suspension of small particles—such as dust specks or liquid droplets—within a gas. A common model for such systems is a Vlasov-Euler type system, where the coupling occurs through a drag force and the volume fraction of the fluid. We study the linearised system around reference states and we prove that sound waves interact with particles of nearby velocities, which results in a damping or an amplification of these sound waves, depending on the sign of the derivative of the distribution function at the sound speed. This is a work in collaboration with D. Bian, C. Buet, B. Després and E. Grenier. Title: Recent advances in the mathematics of the almost-bosonic-extended-anyons gas Abstract: In this talk I will introduce the topic of the anyon gas within its almost-bosonic extended framework. I will then focus on the usual N-body properties of the gas, such as its ground state and coherence, and review recent mathematical results related to these subjects. Title: The fully discrete JKO scheme for nonlinear diffusion and crowd motion models Abstract: The theory of gradient flows in the space of probability measures provides powerful tools for studying a broad class of evolutionary equations. The JKO scheme (a particular case of the minimizing movement scheme) plays a crucial role in this theory, serving as a counterpart to the implicit Euler scheme for classical gradient flows. The JKO scheme provides a means to study well-posedness and to develop numerical schemes for equations of interest. This talk presents a formulation of the JKO scheme restricted to atomic measures on the regular grid as a discrete-in-space approximation to the standard JKO scheme. We discuss the application of this fully discrete formulation for developing new numerical schemes for nonlinear diffusion equations with drift and the crowd motion model. The main result of this presentation is the convergence of the scheme to the corresponding PDEs as the time and space discretization vanish. This is joint work with Filippo Santambrogio. Title: Payne’s nodal line conjecture fails on doubly-connected planar domains Abstract: We will construct bounded planar domains with one single hole for which the nodal line of a second Dirichlet eigenfunction is closed and does not touch the boundary. This shows that Payne’s nodal line conjecture can at most hold for simply-connected domains in the plane. Depending on the time available, we will also mention the case of Neumann boundary conditions. Title: Derivation of the Monokinetic Vlasov-Stokes equations. Abstract: This talk is based on a recent joint work with Richard Höfer (University of Regensburg) and Richard Schubert (University of Bonn). We consider a microscopic model of spherical particles with inertia in a Stokes flow. As the particle number grows to infinity and their size goes to zero we derive the monokinetic Vlasov-Stokes equations as mean-field limit using the 2-Wasserstein distance. We assume that the particles have initial velocities given by a Lipschitz velocity profile and prove the mean-field limit for times of the order of the inverse Lipschitz constant. The proof combines the method of reflections used for Stokes homogenization problems in perforated domains with Hauray's method for mean-field limits. Title: Evolution PDEs & semigroup techniques Abstract: Je présenterai un panorama de techniques de semi-groupe qui permettent d’obtenir pour certaines EDP d’évolutions des résultas de retour vers l’équilibre, parfois avec taux optimal, et d’existence de solutions globales dans un régime perturbatif autour de l’équilibre. Title: Some optimization problems for bistable reaction-diffusion equations Abstract: In this presentation, I will describe several results concerning the following typical problem: how to minimize the L1 norm of an initial datum u0 while ensuring that the solution of ut-uxx= u(1-u) (u-θ) departs from the equilibrium state 0? Several results have been obtained with A. I. Toledo and I. Mazari for a variant of this problem in finite time. In the case of an infinite horizon, the optimal initial data can be characterized via an adjoint problem whose definition is far from trivial. Several applications will be proposed. Title: Non-uniqueness and recovery of uniqueness for the transport equation Abstract: In 1989, DiPerna and Lions established well-posedness of the transport equation for bounded weak solutions for Sobolev vector fields. In 2004, Ambrosio further proved well-posedness for bounded weak solutions when the vector field is of bounded variation. Both works also give an almost everywhere unique flow under a quasi-incompressibility condition. I will discuss a recent construction of Sobolev vector fields with highly non-unique integral curves. I will further discuss the case of vector fields whose bounded variation norm is singular at the initial time, and explain how uniqueness can be recovered, both at the Eulerian and Lagrangian level, even though bounded weak solutions are non-unique. Title: Filamentation near monotone zonal vortex caps Abstract: We study the Euler equations on a rotating unit sphere, focusing on the dynamics of vortex caps. Leveraging the L^1-stability of monotone, longitude-independent (i.e. zonal) profiles, we demonstrate a generic instability phenomenon characterized by the linear time growth of the interface perimeter for vortex cap solutions. We consider configurations that are nearly equivalent in area to a zonal vortex cap but are perturbed by a localized latitudinal bump. By comparing the longitudinal flows at points along the zonal interface and within the bump region, we track the induced stretching and capture the underlying instability mechanism.
Title: Spectral inequality and heat observability on non-compact manifolds. Abstract: Since the work of Lebeau--Robbiano, it is known that inner controllability of the heat equation holds from subsets satisfying a so-called spectral inequality: the L2 norm of eigenfunctions (or more generally, of functions with compact spectral support) must be bounded by their L2 norm on the subset, with a constant growing exponentially with the frequency. In joint work with Alix Deleporte and Jean Lagacé, we characterize the sets for which such an inequality holds on non-compact manifolds satisfying some curvature bounds. The necessary and sufficient condition is known as thickness, meaning the set must intersect every geodesic ball with measure bounded from below, proportionnally to that of the ball itself. The spectral inequality we derive depends only on curvature bounds rather than on the metric itself. In the talk, I will explain how thickness and the spectral inequality interact with geometric features, and why the thickness assumption is sharp. The tools at stake draw from harmonic and geometric analysis. Title: Semi-classical limit for Klein-Gordon equations Abstract: Quantum mechanics is well approximated by classical physics when Planck's constant is considered small, i.e., in the semi-classical limit. Typically, one can study an observable associated with a particle, such as its momentum or its position, and show that its dynamics is given by classical dynamics at first order, with corrections of the order of Planck's constant. In this talk, I will present more precisely the concept of semi-classical limits, the standard mathematical results known for non-relativistic quantum mechanics, and my work that concerns the semi-classical limit in the context of relativistic quantum mechanics. Concretely, I will show how to adapt the modulated energy method to Klein-Gordon equations and how to recover relativistic mechanics (instead of classical mechanics) at the semi-classical limit. Title: Local Hyperbolic Structure in the Water Jet System Abstract: The instability of the water jet system under long-wave perturbation—the Rayleigh-Plateau instability—has been observed and studied in experimental and theoretical physics since the 19th century. This presentation provides a rigorous mathematical justification for this phenomenon. We consider the water jet system, modeled by the incompressible irrotational Euler equation with surface tension, and prove that it possesses a hyperbolic structure around the zero solution. The core of our method involves paradifferential calculus for conjugation in order to decouple this quasilinear system. This reduction enables the use of Lyapunov-Perron type arguments to construct the stable/unstable manifolds and a center invariant set. To our knowledge, this result is the first justification of (local) hyperbolic structure for a quasilinear PDE system, offering a novel method potentially applicable to other quasilinear equations. This is a joint work with Chengyang Shao. Title: Spreading Properties of a City-Road Reaction-Diffusion Model on One-Dimensional Lattice Abstract: We consider a City-Road reaction-diffusion model to describe spreading dynamics on the lattice. The model consists of cities interconnected by a transportation network, such as roads, railways, or rivers. We investigate the existence and uniqueness of the Cauchy problem and characterize the existence of stationary solutions. Furthermore, we analyze the asymptotic spreading speed, highlighting the influence of various parameters on the propagation dynamics. |